hbeLabs.com

Sweep completed on December 14, 2016.

Sweep data ($\delta\lambda\approx\pm 0.1$) for lowest 164,300+ eigenvalues
  Unit-edged Regular Pentagon, both Dirichlet and Neumann boundary conditions

Bob Jones
Summer 2016

This page simply lists the eigenvalues corresponding to each boundary condition (Dirichlet D or Neumann N) within each symmetry class (A,B,C,S) for the regular pentagon, i.e., the values of $\lambda$ which are solutions to $$ (\Delta+\lambda)\Psi(\mathbf{r}) = 0\qquad\mbox{in $\Omega$, with} \qquad\mbox{D: } \Psi=0\quad\mbox{or}\quad \qquad\mbox{N: } \frac{\partial\Psi}{\partial n}=0 \qquad \mbox{on $\partial\Omega$} $$ where $\Omega$ is the unit-edged regular pentagon, $\partial\Omega$ is its boundary, and $n$ the outward pointing normal.

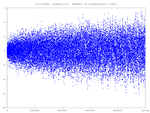
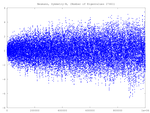
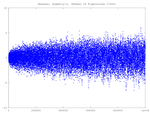
I also include Weyl counting function plots which provide some numerical evidence that this set of numbers is complete.

Since the edge-length of the regular pentagon is one, the lowest Dirichlet eigenvalue is about 11.00. Also of note, for this tally, I do include the trivial NS $\lambda=0$ eigenvalue.

The total number of distinct eigenvalues with $\lambda<10^6$ is $$ \#(10^6) = \#_\mathrm{D}(10^6) + \#_\mathrm{N}(10^6) = 81,913 + 82,360 = 164,303 $$ where $\#(\lambda)$ counts the number of distinct eigenvalues less than $\lambda$ (here a continuous parameter).

In addition, for each of the eight towers, I include the next one up beyond $\lambda=10^6$, making a total of 164,311 eigenvalues displayed on this page.

For a glimpse of what the four symmetry classes (A,B,C,S) look like, the plots of the eigenfunctions for the lowest 802 Dirichlet eigenvalues here.

I used the GSVD method to sweep over the interval $\lambda=0$ to just over 1,000,000. I used various but related methods to identify the eigenvalues by watching the smallest singular value as I "swept" over the interval from $\lambda=0$ to $10^6$.

Actual number of distinct Dirichlet eigenvalues with $\lambda< 1,000,000$: $$ 13531+27302+27304+13776= 81,913$$

Actual number of Dirichlet eigenfunctions with $\lambda< 1,000,000$: $$ 13531+2(27302+27304)+13776= 136,519$$

Weyl's two term counting formula (disregarding constant term) for Dirichlet eigenvalues: $$ N_w(10^6) = \frac{1}{4\pi}\,\left\{ A \times (10^6) - 5 \times (10^3)\right\} = 136,513.4$$ where $A=10\tan(3\pi/10)/8\approx 1.7204774005$ and 5 are the area and perimeter of the pentagon.

Actual number of distinct Neumann eigenvalues with $\lambda< 1,000,000$: $$ 13610+ 27460 + 27464 + 13856 = 82,390 $$

Actual number of Neumann eigenfunctions with $\lambda< 1,000,000$: $$ 13610+ 2(27460 + 27464) + 13856 = 137,314 $$

Weyl's two term counting formula (disregarding constant term) for Neumann eigenvalues: $$ N_w(10^6) = \frac{1}{4\pi}\,\left\{ A \times (10^6) + 5 \times (10^3)\right\} = 137,309.2$$ where $A=10\tan(3\pi/10)/8\approx 1.7204774005$ and 5 are the area and perimeter of the pentagon.

Total of Dirichlet eigenvalues in these lists $= 81,917$
DA DB DC DS
(13,532) (27,303) (27,305) (13,777)

[L.DA.dat]
[L.DB.dat]
[L.DC.dat]
[L.DS.dat]
Total number$^\dagger$ of Neumann eigenvalues in these lists $= 82,394$
NA NB NC NS
(13,611) (27,461) (27,465) (13,857)$^\dagger$

[L.NA.dat]
[L.NB.dat]
[L.NC.dat]
[L.NS.dat]
${}^\dagger$ Tally includes $\lambda=0$ in the NS list.

Weyl Plots

See Weyl Counting Function and Plots for more information. The graphs above are described briefly here: These plots---and more profoundly, the L vs cumsum(d) plots---are extremely helpful in detecting missing or inadvertently added eigenvalues.
Of course the constant term cannot be disregarded, but it is typically on the order of unity, and is actually quite simple for each symmetry class.
Finished Wed Dec 14, 2016
(Mon May 30, 2016, first posted with some missing data.)
rsjones7 at yahoo dot com