Note: This begins [with DS] January 1, 2017.
Note: This resumes with NS January 30, 2019
Note: This starts with DA February 4, 2019
NA complete, Feb 26, 2019 to Sep 24, 2019.
100-digit eigenvalues - the regular pentagon
Unit-edged Regular Pentagon, both Dirichlet and Neumann boundary conditionsBob Jones
Winter 2017This work is a numerical refinement of the initial GSVD sweep results.
The numbers on this page are the values of $\lambda$ to solutions of the Helmholtz problem $$ (\Delta+\lambda)\Psi(\mathbf{r}) = 0 \qquad\mathbf{r}\in\Omega , \qquad \mbox{D: }\Psi(\mathbf{r})=0\quad \mbox{or}\quad\mbox{N: } \frac{\partial\Psi}{\partial n}(\mathbf{r})=0 \qquad \mathbf{r}\in\partial\,\Omega $$ inside $\Omega$, the unit-edged regular pentagon, subject to either Dirichlet D or Neumann N boundary conditions on the pentagon's boundary $\partial\,\Omega$, where $n$ is the outward-pointing unit normal vector.
DA eigenvalues
$\#(806,004) = 10892 =\mbox{tally}$
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$
[L.DA.100.dat]DS eigenvalues
$\#(544,548) = 7514 =\mbox{tally}$
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$
[L.DS.100.dat]NA eigenvalues
$\#(541,061) = 7349 =\mbox{tally}$
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$
[L.NA.100.dat]NS eigenvalues (here excluding the important but trivial $\lambda=0$)
$\#(1,000,117) = 13856 =\mbox{tally}$
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$
[L.NS.100.dat]
The solutions are classified according to the dihedral symmetry of the regular pentagon, which creates the four symmetry towers (A,B,C,S). Since $10=1^2+1^2+2^2+2^2$, for a given boundary condition, there are two non-degenerate towers (which I call A and S) and two doubly degenerate towers (which I call B and C). See plots for a visual meaning of this symmetry classification. I use the following abbreviations for the eight towers of distinct eigenvalues:
DA DB DC DS NA NB NC NS (Note: red means they are currently being calculated. Bold means I stopped computing them [for now]. green means that [finite] tower is computed.)
The eigenvalues are calculated to at least 105 digits, then truncated (not rounded) at 105 digits, so all of these digits are presumed to be correct.
The html "textarea" displays a few header rows to help count digits, and the result of "$ nl L.*.100.dat", but the linked-to file[s] include neither that header nor the line numbers.
As described in more detail below, the staircase counting function is $$\#(\lambda)=\mbox{number of eigenvalues less than $\lambda$} $$ and the well-known Weyl's two-term (or is it three-term?) counting function is $$ N_W(\lambda) = C_1 + C_2\lambda + C_3\sqrt{\lambda} $$ where the $C$s are constants.
Some details
Weyl counting formulas
To ensure that there are no missed or extra numbers in my eigenvalue list, a plot of the difference between the asymptotic Weyl counting formula $N_W(\lambda)$ and the actual numerical staircase counting function $\#(\lambda)$ [number of eigenvalues less than $\lambda$] is plotted. That difference is $$ \mathrm{d}(\lambda) = N_W(\lambda) - \left(\#(\lambda) - \frac{1}{2}\right) $$ where the (often not-mentioned) additive factor of 1/2 is to ensure the mean of $\mathrm{d}(\lambda)$ is zero.
Each eigenvalue tower has its own Weyl counting function,
Mode $N_W(\lambda)$ DA $\frac{7}{18} +\frac{1}{2} + \frac{1}{4\pi}\, \left[A\lambda - P \sqrt{\lambda}\right]$ DS $\frac{1}{18} + \frac{1}{2} + \frac{1}{4\pi}\, \left[A\lambda + (P-1)\sqrt{\lambda}\right]$ NS $\frac{7}{18} -\frac{1}{2} + \frac{1}{4\pi}\, \left[A\lambda + P\sqrt{\lambda}\right]$ In the table above, $P$ and $A$ are the perimeter and area of the fundamental domain of the unit-edged regular pentagon, i.e., the 36-90-54 triangle with shortest edge equal to 1/2, $$ H=\frac{1}{2}\, \tan\left(\frac{3\pi}{10}\right) \qquad\qquad P = \frac12 + H + \sqrt{\left(\frac{1}{2}\right)^2 + H^2} \qquad\qquad A = \frac{1}{8}\,\tan\left(\frac{3\pi}{10}\right) $$
For the full unit-edged regular pentagon, the Weyl counting formula is $$ N_W(\lambda) = \frac{5}{9} + \frac{1}{4\pi}\left( 10A \lambda \mp 5 \lambda \right) $$ where $-$ and $+$ are used for Dirichlet and Neumann modes, respectively; where $A$ is as above, but the pentagon has ten times the area of the fundamental region, and its perimeter is five; and the additive factor is due to the corners, specifically, $$\frac{1}{24}\sum_{i=1}^{5}\left(\frac{\pi}{[3\pi/5]}-\frac{[3\pi/5]}{\pi} \right)= \frac{5}{24}\left(\frac{5}{3}-\frac{3}{5}\right)=\frac{5}{9}$$
The eight eigenvalue towers have their respective factors, but they must all add up to match that of the full pentagon. Sometimes, the additive factor can be calculated by considering other symmetry-related shapes with pure Dirichlet or Neumann boundary conditions. Alternatively, to figure out that constant, first set it equal to zero and then equate it to the mean of $\mathrm{d}(\lambda)$.
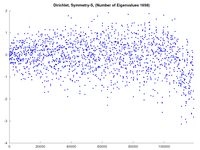
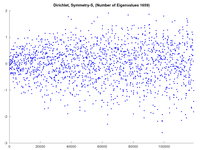
Why are the plots useful? It seems that $\mathrm{d}(\lambda)$ is an interesting but random-looking function. However, even one missing (extra) number in the eigenvalue list will be revealed as a step down (up) in $\mathrm{d}(\lambda)$ at the site ($L$-value) of the mistake, even if there are very many numbers in that list.
A "nice" $\mathrm{d}(\lambda)$ plot reveals that all of the eigenvalues are included, but it doesn't actually prove they are the actual eigenvalues since, for example, shifting them all a small amount (say up to $\pm 1\%$ of the mean eigenvalue gap) would not indicate missing or extra numbers in the list.
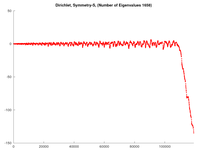
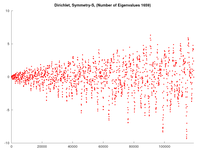
The matlab/octave command "plot(L,cumsum(d))" is actually much more useful in visually identifying that "mistake" in the list. In the above diagrams. Of course, if there is a mistake, I try to find and fix it. (See below for an example of a failure, and how dramatically different the cumsum plot looks.)
Also note that the cumsum plot more clearly reveals a growing regularity as $L$ increases due to an approximate symmetry giving rise to approximate "bouncing ball" and other periodic orbits within the regular pentagon.
Example: Below, with the first row of pictures, is an example when it skipped DS-1523, $\lambda=109,302.817$. The initial sweep did find it as $109,303.1$, so it was just a little bit too far away for this program to find it. The step by "-1" in $\mathrm{d}(\lambda)$ is barely noticeable compared to the dramatic change in its cumsum. The second row of figures shows what happened when I ensured this eigenvalue wasn't skipped.
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$
$\mathrm{d}(\lambda)=N_w(\lambda)-\#(\lambda)$
cumsum($\mathrm{d}(\lambda))$Convergence
The formula for stepping through $N$ values depends on how high up the tower we are, and this formula is crucial to calculating high eigenvalues to a limited precision like 100 digits.
It ironically becomes more difficult to calculate as few as 100 digits way up the tower because the convergence rate is so good, specifically, the starting N value might be so high as to give more than 100 digits in the eigenvalue bound.
I find that, on the one hand, equal-spaced matching points yield poor convergence, but exhibit the alternating property at low N-values. This means that it is numerically easy (relatively low matrix sizes) to obtain easy-to-identify bounds much tighter than starting estimate ($\Delta\lambda\lt\pm 0.5$).
On the other hand, Chebyshev distributed matching points yield excellent convergence, but they do not exhibit the alternating pattern until much higher N-values (about 7/3 times higher than equal space matching points for this example).
As a compromise, I begin the process with equal-spaced matching points to get a low resolution result (perhaps 8 to 20 digits), then switch to either a mixture of Chebyshev and equal-spaced point, or a pure Chebyshev distribution. As I climb the tower, the starting N-value increases making it more and more difficult to get that initial estimate (from the sweep result).
For the DS modes, the alternation begins at about $$ N_\mathrm{beg} = c \frac{Y_\mathrm{max}}{\Lambda} $$ where $Y_\mathrm{max}=(1/2)\tan(3\pi/10)$ is the length of the unit-edged regular pentagon apothem (point-matched edge) and $\Lambda=2\pi/\sqrt{\lambda}$ is the wavelength. The factor $c$ is numerically determined, and (for the DS modes) is about $c=3.00$, which seems valid from the lowest to the highest $\lambda=0$ to $10^6$ in my set of eigenvalues.
That constant $c$ for the Chebyshev matching points is just over 7, which means the alternation doesn't appear until much higher $N$ values, which means that above a certain value of $\lambda$, it is not possible to get pure alternation ($+-+-+-+-+...$) if we want an easy-to-identify hundred digit eigenvalue based on that alternation. However, if I use a tradeoff (linear combination of linear spaced and Chebyshev matching points), I can get acceptable convergence rates and alternation, allowing me to get that easy-to-identify bound at just over 100 digits.
The following shows what a typical calculation looks like. In this example, the starting estimate for the 518th DS eigenvalue is $\lambda=36598.10\pm 0.1$. Equal spaced matching points with $N=63$ and $N=64$ are used to get a "rough" 19-digit estimate $\lambda=36598.11576305836797\,_{69}^{74}$. Then, the distribution is changed to (in this case) "0.2 Equalspaced+0.8 Chebyshev", and $N$ is incremented a few times. When the right pattern of alternation appears, eg. $(+-+-...)$, a bound is calculated and used to predict the N-value needed for (just over) 105 digits. That $N(D)$ is the linear regression of the most recent bounds found for this calculation. I am somewhat cautious when incrementing $N$ and identifying the bound. Until I reach the desired number of correct digits, the best bound found is used as a starting point in my search for the more precise root of the point-matching matrix at that higher N-value.
[Higher up the tower, I found that estimating the next N value is much easier using the simple relationship that $N/D$ is constant (once I have a bound).]
In the end, the five most recent calculations must correctly alternate for it to be considered a bound calculation. Something like $(+-+-+...)$ must happen, but each time it alternates, it must also properly converge. Thus, if the tail of the sequence of calculated $L$ values is $$\{\cdots, L_1, L_2, L_3, L_4, L_5\} $$ then the true eigenvalue $\lambda$ is bounded with one of $$ L_1 \lt L_3 \lt L_5 \lt L_4 \lt L_2 \qquad\Rightarrow\qquad L_5\lt\lambda\lt L_4 $$ or $$ L_2 \lt L_4 \lt L_5 \lt L_3 \lt L_1 \qquad\Rightarrow\qquad L_4\lt\lambda\lt L_5 $$ where the bound is formed with the last two calculated L values. For this to work, the N-values for the last two must satisfy $N_5-N_4=1$.
In the example below, the bound is formed with the $N=160$ and $161$ calculations, which yields 111 correct digits. Although not computationally elegant, it is more CPU time consuming to try to hit an exact target than to overshoot a few digits.
This eigenvalue took 138 seconds (i7, 6-core), and most of the time was spent from $N=91$ to $95$, waiting for the alternation pattern.
Of course, as indicated above, the final answer is truncated (the trailing correct digits "282971" are simply discarded) and reported to 105 digits as
36598.11576 3058367977 5294323176 5021292714 7905429092 9330611926 5838419926 8592712003 4329810937 7995618070 35415 282971
Below is another example, DS-1476, a bit higher up and with a few refinements to the N-value incrementing. Note that I had to make the mixture of matching points more like (0.3 EqualSpaced+0.7 Chebyshev). That compromise in convergence in favor of the alternating pattern actually makes the elapsed time quite small (about three minutes).